Geometri için alan hesabını doğru yapabilmek son derece önemlidir. Soruların doğru şekilde yanıtlanması için alan hesaplamasını dikkatli yapmak gerekmektedir. Özellikle altıgenin alanı nasıl bulunur sorusu bu alanda çok merak edilmektedir.
Altıgenin Özellikleri
Altıgen özellikleri geometride sıklıkla karşınıza çıkacaktır. Özellikle düzgün altıgen hem ortaöğretim müfredatında hem de üniversite giriş sınavında sıklıkla sorulmaktadır bu yüzden altıgeni bilmek çokgenler konusunda soruların nasıl çözüleceği hakkında da bilgi verecektir. Altıgen özellikleri şu şekildedir;
- Altıgen adından anlaşıldığı altı kenardan oluşmaktadır. Bunun sonucunda da altı köşesi bulunmaktadır.
- Altıgen iç açıları toplam dereceleri 720 derecedir. Bu durum da (n-2).180 formülü ile bulunmaktadır.
- Tüm çokgenlerdeki gibi altıgenin dış açıları toplamı 360 derecedir.
- Altıgende dokuz tane köşegen bulunmaktadır. Bunun formülü n.(n – 3) / 2 olarak bulunmaktadır.
Düzgün altıgen özellikleri olarak aynı zamanda şu özelliklerinin de bilinmesi gerekmektedir;
- Tüm kenar uzunlukları eşit olmaktadır.
- Tüm iç açıları eşittir ve bu yüzden her bir iç açı 120 dereceye sahiptir.
- Tüm dış açı ölçüleri eşit olmakta ve her bir dış açı 60 dereceye sahiptir.
- Kenar uzunluğu a olan bir altıgenin çevresi 6.a = 6a şeklinde bulunmaktadır.
- Kenar uzunluğu a olan bir altıgen kenar uzunluğu a ise 6 tane eşkenar üçgenin birleşmesi ile oluşmuştur.
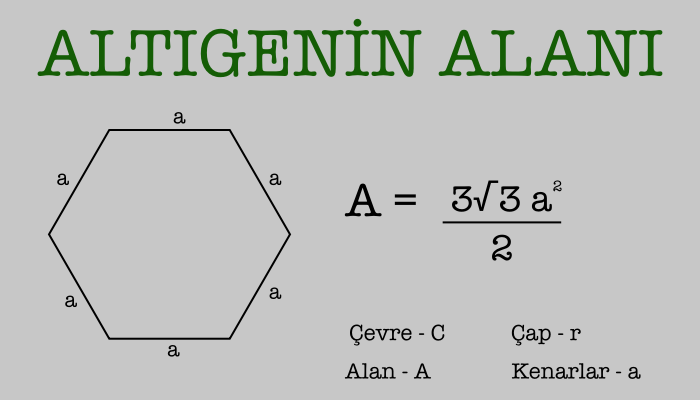
Altıgenin Alanı Nasıl Hesaplanır?
Altıgenin alanını bulmak için formül kullanmak gerekmektedir. Düzgün olmayan altıgen alanı bulmak için çeşitli bölgelere ayırmak gerekmektedir. Düzgün altıgenin alanını ise formül kullanarak bulmak mümkündür. Düzgün altıgenin temel özelliklerinden birisi 6 adet eşkenar üçgenin bir araya gelmesi ile ortaya çıkmasıdır. Bu bakımdan eşkenar üçgen alan formülü ve 6 çarpıldığında düzgün altıgenin alanı ortaya çıkacaktır. Bu bakımdan altıgen alan bulma formülü 6.(a(2).√3/4) şeklindedir. Bu formüldeki 6 sayısı 6 tane üçgeni çarpımdan sonraki kısım ise eşkenar üçgen alan formülünü vermektedir. Bu bakımdan 6 tane üçgen x eşkenar üçgen alan formülü ile altıgenin alanı bulunmaktadır. Eğer üçgen formülünü hatırlamazsanız bu durumda bir eşkenar üçgen çizerek dikme indirip formül çıkarmak da mümkündür.